1. Concept/Principle
2. Scale on X-axis
3. Scale on Y-axis
4. Finding 30% brides
5. Practice questions

In a marriage hall 120 marriages were held in a particular year. The age distribution is as shown below Determine the maximum age among youngest 30% of brides.

Age	No. of Brides
18-20	12
20-22	30
22-23	30
23-24	22
24-26	18
26-28	8

Concept/Principle

Original question: Determine the maximum age among youngest 30% of brides.
Let me rephrase the question.

• In hall, 120 brides are standing in ascending order of their age (20..23…25 and so on)
• The first 30% brides =120 x 0.3=36 brides.
• The age of these 36 brides, is less than “m” years. Find “m”

The situation calls for a cumulative frequency (CF) graph.

Make a new column

Age	No. of Brides	c.f. (less than)
18-20	12	0+12=12
20-22	30	12+30=42
22-23	30	42+30=72
23-24	22	72+22=94
24-26	18	94+18=112
26-28	8	112+8=120

This is cumulative frequency “less than” graph.
Observive first cell of “CF”, it has number 12
It means 12 girls have age less than 20 years.
Similarly 42 girls have age less than 22 years and so on.
Now make a cumulative frequency graph, with Age in years on X-axis and C.F. on Y-axis
Basically we’ve to plot these following numbers:

Age less than (X axis)	No of brides (Y axis)
20	12
22	42
23	72
24	94
26	112
28	120

Now the biggest problem: (stupid) scales.
A typical graph paper has drawable area of 25 x 19 cm.
We want the graph to be evenly ‘spread’ across the paper, we don’t want a very small graph else we cannot find exact answer.

Scale on X-axis

• X axis= minimum observation is 20 and max is 28. So we’ve to plot 28-20=8 years.
• If we take 1cm=1 year, then entire data can be plotted in 8 cm.
• but then graph will look too small and narrow.
• So let’s increase the scale. Instead of 1 cm=1 year, let’s take 2 cm=1 year.
• In that case, to plot 8 years, we’d need 16 cm.
• Our graph paper can easily accommodate this, because we have 25x19cm paper.
• Therefore, scale on x axis: 2cm =1 year (or 1cm=0.5 year).

Scale on Y-axis

• Difference between maximum and minimum observation: 120-12=108 brides.
• How about 1 cm =5 brides?
• To plot approx 110 brides, we’d need 110/5=22 cm. Again Our graph paper can easily accommodate this because we’ve 25×19 cm paper.
• So we take scale on Y axis: 1 cm=5 Brides.
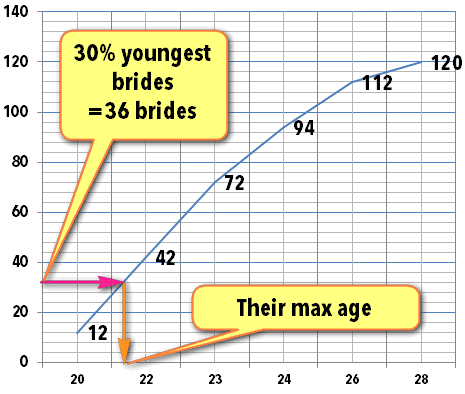
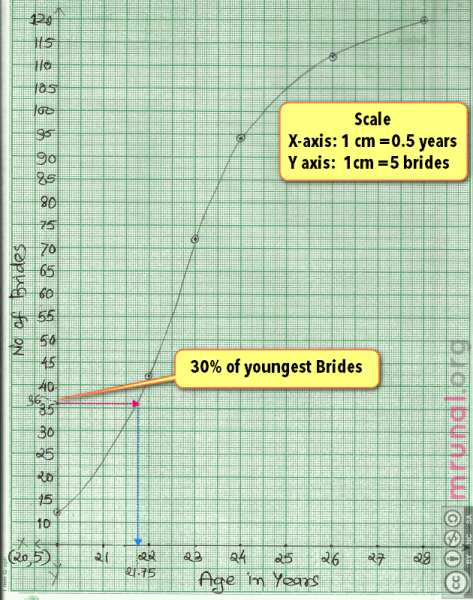
• Now plot those numbers. It’ll look something like this image:

Finding 30% brides

The question says “maximum age among youngest 30% of brides”
Total brides=120, and in the graph paper, we’ve plotted them in ascending order (age is going on like 20….22…23…)
30% of total brides
=120 x 0.3
=36 brides
On the Y-axis, locate number 36 then draw a parpendicular line from that number to the cumulative frequency graph. (Pink colored line going towards right side.)
It will cut the cumulative frequency line somewhere.
From that point, draw anohter parpendicular line towards X-axis (blue line going downwards).
The point at which it cuts X-axis= our answer.
In above graph, it cuts at 21.75 years.
Therefore answer: maximum age among youngest 30% of brides is 21.75 years.

Practice questions

In a marriage hall 120 marriages were held in a particular year. The age distribution is as shown below:

Age	No. of Brides
18-20	12
20-22	30
22-23	30
23-24	22
24-26	18
26-28	8

Find following

Question	Concept Explained in this youtube video
Find Average age of brides	http://www.youtube.com/watch?v=FC8CQGY1CUE&feature=plcp
Find median Age of brides using formula graph	http://www.youtube.com/watch?v=uaHBu2kz8pM&feature=plcp
Find modal age of brides	http://www.youtube.com/watch?v=BUdd3-PBe6Q&feature=plcp
Find Standard Deviation of the data.	http://www.youtube.com/watch?v=boHDPTX5YnU&feature=plcp

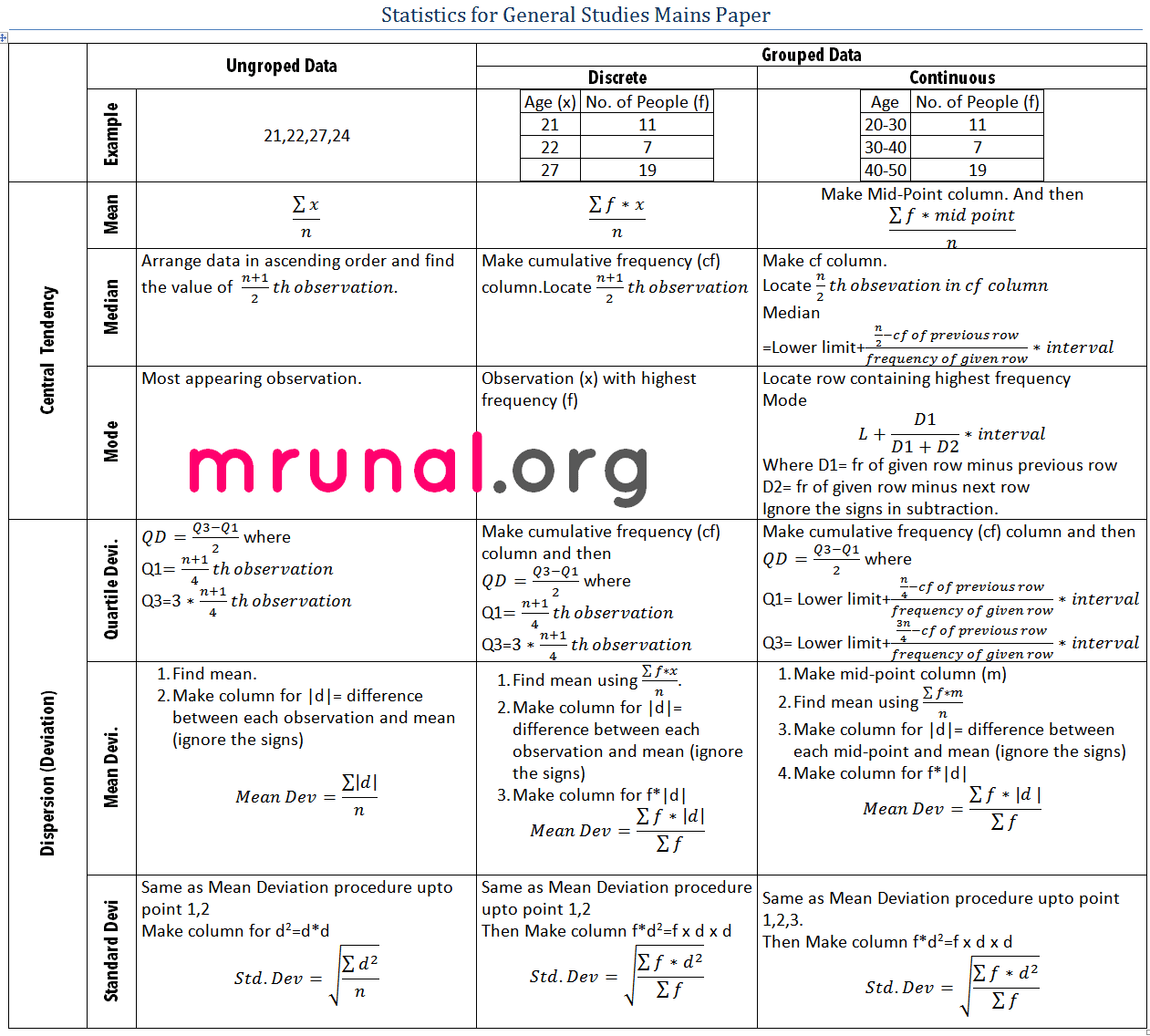
Basically this is a “Continuous Data Series”. So, use this ready-reference Statistics formula table to solve above questions accordingly: