- Introduction
- Table based Questions
- Case1: finding value
- Case2: multiplication chain
- Case3: finding angle
- Mock Questions
Introduction
For SSC CGL trigonometry, there are mainly four types of questions
- Height and distance: and it has five subtypes. We already saw how to solve them. If you haven’t seen it, click on my youtube playlist
- Table based: Finding values and angles: We will see this in today article.
- Complimentary angles (90-A): discussed in separate article click me.
- Trigonometry formulas + algebraic formulas: to be released.
Table based Questions
Here is an example of Table based questions:
- What is the value of 3cos230+sec230+2cos-+3sin90-tan290
- If sinA=2sin30*cos30, then find value of A
- To solve these type of questions, you must know the “table” (=meaning the values of sin, cos, tan, cosesc, sec and cot for 0, 30, 45, 60 and 90 degree angles).
- From the earlier youtube video, you already know the shortcut technique to memorize the values of 30, 45, 60 of sin, cos, tan, cosec, sec, cot, using those two “topi triangles”. (if not click me)
- Today we’ll extend it further and create the whole table from 0 to 90 degrees.
| 0 | 30 | 45 | 60 | 90 | |
| Sin | |||||
| Cos | |||||
| Tan | |||||
| Cosec | |||||
| Sec | |||||
| cot |

First using above “Topi triangles” I’m going to fill up the values of Sin, cos, tan for 30, 45 and 60 degree angles. (sin = opp/hypo, cos=adj/hypo and tan=opp/adj)
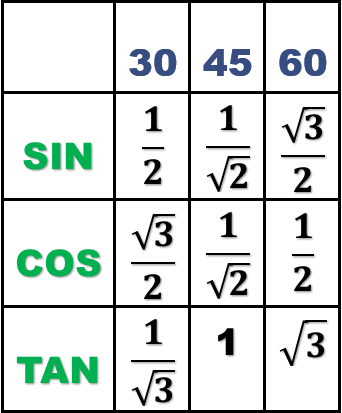
but we know know that
- sin = 1/ cosec. That means for cosec 0 to 90, I’ll just inverse the values of sin 0 to 90. (e.g. sin30=1/2 means cosec30 will equal to 2)
- Cos=1/sec. that means for sec 0 to 90, I’ll just inverse the values of cos 0 to 90. (e.g. cos60=1/2 therefore sec60=2).
- Tan=1/cot. That means for cot 0 to 90, I’ll just inverse the values of tan 0 to 90 (e.g. tan45=1, so cot45 will also be 1).
Here is the updated table. (don’t just read this, keep making the table in your notebook/rough paper simultaneously).

Ok so far, we’ve filled up all the values for 30, 45 and 60. Only two column remain: 0 degree and 90 degree. That can be filled up very quickly if you just remember two things
- For zero to ninety, sin is 0 to 1. And the case of cos is reverse (meaning for zero to ninety, cos is 1 to 0).
- Zero’s inverse (1/0)=not defined. And vice versa (meaning “1/not defined” = 0).
- Applying the first rule: for 0 to 90, sin is 0 to 1, and cos is 1 to 0.
- WE also know that Tan=sin/cos.
- So tan0=0/1=0 and
- tan90=1/0=Not defined
- now we’ve the values of sin, cos and tan for 0 degree angle and 90 degree angle. We can inverse them and get the values for cosec, sec and cot also. (recall rule number two: 1/0=not defined and not defined’s inverse is 0).
Finally we’ve our table ready.

I suggest you construct this table on your own for atleast 2-3 times at home. Otherwise this technique will not go in long term memory.
In the exam you don’t have to create the whole table in the rough paper, just get only those values that are required for the given question. Now let’s try some Table based Questions.
Case1: finding value
Q. Find value of sin60*sin45+cos60*cos45
- Just Plug in the values into the given equation
- Answer will be (root6+root2)/4
Q. if cosA+cosB=2 then find value of sinA+SinB, given that both angle A and B are between 0-90 including both 0 and 90.
- Ans. If you look at the table, cos0+cos0=1+1=2. That means both A and B angles are 0 degree angles.
- Therefore SinA+SinB=Sin0+sin0=0+0=0.
Q. Find the value of cos25/sin65.
- We only know the table for 0, 30,45,60 and 90. We don’t know the tables for 25 or 65. Don’t worry, these questions are based on the formula of complimentary angles. We’ll learn that in next article.
Case2: multiplication chain
Q. find the value of tan0 x tan1 x tan2 x tan3x….tan89
Approach: from the table we know that tan0=0. So no matter what you multiply with zero, final answer will always be zero.
Q. find the value of cos2 x cos4 x cos6 x cos8x….x cos92
Approach: as you can see the angles are increasing as per the multiplication table of 2. So in the chain, you’ll also get cos90 (because 2 x 45=90). So we can write the chain as
cos2 x cos4 x cos6 x cos8x….cos88 x cos90 x cos92
but we know that cos90=0, hence the whole multiplication will become zero.
Q. find the value of tan48 x tan 23 x tan 42 x tan67
Approach: as you can see there is no tan0 in this multiplication chain (otherwise we could get zero as the answer.) but this question can be easily solved using the formula of complimentary angles. (we’ll see it in the next article).
Case3: finding angle
Q. For 0<A<90, if sinA=sin60 x cos30-cos60 x sin30, then what is the value of A?
- 0
- 30
- 45
- 90
Approach:
| left hand side LHS | right hand side RHS |
| sinA= | sin60 x cos30-cos60 x sin30 |
| Plug in the values and you get right hand side is 1/2 | |
| sinA= | 1/2 |
Now go back and observe the table. In the Sin’s row, You see the sin30=1/2. Therefore, A=30 degrees.
Q. If Sin(A+B)=root3/2 and SIN(A-B) =1/2 then what are the values of A and B? (given that both A and B are acute angles and A>B)
- 30,60
- 45,45
- 45,15
- None of above.
Approach
- Sin(A+B)=root3/2 (this is given in the question itself).
- If you look at the table, sin60=root3/2. That means A+B=60…eq1
- Similarly we’ll get A-B=30….eq2
- So we’ve two equations:
- A+B=60
- A-B=30
- Now add these two equations eq1+eq2
- (A+B)+(A-B)=60+30
- 2A=90
- A=45
- Plug this value back in eq1 (or eq2). And you get B=15
- Final answer C: 45,15
Mock Questions
Instructions
- For all these questions, assume that unknown angles are between 0 to 90 (including both 0 and 90).
- Questions about finding values (based on trigonometry table) are easy. You just have to plug in the values and simplify the equation.
- But be sure to observe the rules of simplification (BODMAS) and laws of surds and indices, else you’ll get wrong answer.
- if CosA=1-2sin230, then find value of A
- 30
- 45
- 60
- 90
- if cosA=2cos230-1, then find value of A
- 30
- 45
- 60
- 90
- if cos60=cos2A-sin230, then find value of A
- 60
- 45
- 30
- 90
- if sinA=2sin30*cos30, then find value of A
- 30
- 45
- 60
- 90
- if sinA=2tan30/ (1+tan230), then find value of A
- 30
- 45
- 60
- 90
- if cosA=(1-tan230)/( 1+tan230), then find value of A
- 30
- 45
- 60
- 90
- if cosA=4cos330-3cos30, then find value of A
- 30
- 45
- 60
- 90
- Find value of (5cos260+4sec230-tan245)/(sin230+cos230)
- 67
- 12
- 67/12
- 12/67
- Find value of 3cos230+sec230+2cos0+3sin90-tan260
- 67
- 12
- 67/12
- 12/67
- If sinA=cosA, what is the value of 2tan2A+sin2A+1
- 2
- 7
- 7/2
- 2/7
- What is the value of sinA*cosB+cosA*sinB, if A=30 and B=60
- 0
- 1/2
- 2
- 1
- What is the value of cosAcosB-sinAsinB, if A=30 and B=60
- 0
- 1/2
- 2
- 1
- secA=cosec60, what is the value of 2cos2A-1
- 0
- 1/2
- 2
- 1
- What is the value of 5cos290+3sec230+4cos245+tan260
- 3
- 7
- 5
- 9
- What is the value of 5cos90-cot30+(sin60/cos245)
- 1
- 3
- 0
- 5
- Find the value of (cos30+sin60)/(sin30+cos60+1)
- 1/2
- 1/root2
- Root3/2
- 2/root3
- Find the value of tan260/(sin245+cos245)
- 3
- 1/2
- 2/3
- 1/3
- If cot(A+B)=1/root3 and Cot(A-B)=root3. Find the values of A and B
- 30,60
- 60,30
- 15,45
- 45,15
- Find the value of cos10 x cos20 x cos30 x….x cos90
- 1
- 1/2
- 0
- Not defined.
- If secA-cosecA=0 then find value of secA+cosecA, given that A is an acute angle.
- Root 2
- 2 root 2
- 0
- Not defined
Answers
1)c, 2)c, 3)c, 4)c, 5)c, 6)c, 7)d, 8)c, 9)c, 10)c, 11)d, 12)a, 13)b, 14)d, 15)c, 16)c, 17)a, 18)d, 19)c, 20)b
For more articles on trigonometry and aptitude, visit Mrunal.org/aptitude

![[Reasoning] Calendar Questions: Finding day or date, concepts, shortcuts explained](https://mrunal.org/wp-content/uploads/2013/01/i-lr-500x383.png)
Are these 5 basic types enough for ssc cgl ? Please tell
Mrunal you are GOD for students
Mrunal you are GOD for students
Mrunal you are GOD for students
Mrunal you are GOD for students
Mrunal you are GOD for students
pehle app ko main apne bare me bta du.. I just join tcs.. i am 23 now.. I have 68.8 in 10th and 74.6 in 12th and 65.8 in BE (information technology ) …So what are the option open for me.. you suggest me some thing And I am GEM candidate… i have lots of extra curricular but dont of any importance ….So plz suggest me sum thing related to my profile … and ya i wanna be ias…
What are the options left for me… i am realyy tensed and wanna …suicide..
Mrunal Sir , i want to ask you that whether the theories and problems of Trignometry given by you is sufficient for solving question related to Trignometry in SSC tier 1, i mean will i be able to solve trignometry parts by studying only article given by you …Please reply
This is an awsome & helpful.site for all competative exams aspirants. Thank u very much.
GREAT JOB. . . . . . MRUNAL SIR
plz include few SSC type tricky problems as well.
nice
Mrunal Sir , i want to ask you that whether the theories and problems of Trignometry given by you is sufficient for solving question related to Trignometry in SSC tier 1, i mean will i be able to solve trignometry parts by studying only article given by you …Please reply
question 7…….mine answer 4…
solution plzz??
if cosA=4cos^3(30)-3cos30, then find value of A
cos30=Root 2
so 4*3Root 3/8-3*Root3
3 root 3/2-3 root 3/2=0
cos A is zero if angle is 90
so ander is option d
if cosA=4cos^3(30)-3cos30, then find value of A
cos30=Root 3/2
so 4*3Root 3/8-3*Root3/2
3 root 3/2-3 root 3/2=0
cos A is zero if angle is 90
so ander is option d
I am really thankful to the author and all the guys who had put up their valuable time while explaining such basic but important concepts. Finally I could do these type of questions without much difficulty. Values can’t be forgotten at all now all thanks to the “Topi Triangles” method. Wish my maths’ teacher were this good in explaining these concepts. Thanks a lot again guys. Please keep up with the good work.
Woww! Sir ur explanations in quantitative aptitude are so simple and these are very usefull and in so simplyfied language . I’m very pleased to have this great gadget and teacher on my device ..
thank u sir …u are helping us lot …
if atriangle ,if b+c divide 11=c+a divide 12=a+b divide 13 prove that cosA/4=cosB/19=cosc/25?
can any1 help me with question 13???