Introduction
- Concept of LCM, HCF important for number theory and remainder based problems (generally asked in SSC CGL, CAT.)
- LCM is important for time and speed, time and work problems.
- LCM is also important for circular racetracks, bells, blinking lights, etc.
- HCF is important for largest size of tiles, largest size of tape to measure a land etc.
But before getting into LCM, HCF, let’s understand
What is Prime number?
- Consider this number : 12. This number can be found in many multiplication tables for example
- 1 x 12=12.
- 2 x 6 =12
- 3 x 4=12
- That means, 12 has many factors (1,2,3,4,6,12). Such number is called a composite number.
- On the other hand, consider this number: 29. You cannot find it in any table except 29 x 1 =29. Such number is called a prime number.
- Let’s make a shortlist from exam point of view
| Prime | Non-prime (composite) |
| 2,3,5,7,11,13,17,19,23,29 | 4,6,8,9,10,12,14,15…. |
Now hold this prime number thought in your mind for a while.
What is LCM?
First, let’s create multiplication tables of 4 and 6.
| 4’s table | multiple | 6’s table | multiple |
| 4 x 1 = | 4 | 6 x 1 = | 6 |
| 4 x 2 = | 8 | 6 x 2 = | 12 |
| 4 x 3 = | 12 | 6 x 3 = | 18 |
| 4 x 4 = | 16 | 6 x 4 = | 24 |
| 4 x 5 = | 20 | 6 x 5 = | 30 |
| 4 x 6 = | 24 | 6 x 6 = | 36 |
| 4 x 7 = | 28 | 6 x 7 = | 42 |
| 4 x 8 = | 32 | 6 x 8 = | 48 |
| 4 x 9 = | 36 | 6 x 9 = | 54 |
- Do you see any common numbers in the multiples of 4 and 6?
- Yes I see 12, 24 and 36 are common in both tables. Let’s isolate them.
| 4 x 3 = | 12 | 6 x 2 = | 12 |
| 4 x 6 = | 24 | 6 x 4 = | 24 |
| 4 x 9 = | 36 | 6 x 6 = | 36 |
- Ok so 12, 24 and 36 are common multiples of 4 and 6. But what is the smallest of these multiples? Ans 12 is smallest.
In the exam, we’ve no time to make such ^big tables to find LCM. So how to quickly find LCM of two or three numbers? There are many tricks, the easiest one is prime-factorization. We’ll learn that in a bit, but before that:
LCM4 EXam
- Suppose there is a circular race track. Tarak Mehta takes 4 minutes to finish it and Jethalal takes 6 minutes to finish it. Now both of them start running from the same point at the same time in the same direction. They’ll continue running on this track forever. So after how many minutes will they meet for the first time on the starting point? Ans. LCM of time = LCM (4,6)=12 minutes. They’ll meet again on the starting point after 12 minutes.
- Two bells ring at an interval of 4 and 6 minutes respectively. After how many minutes will they ring together? Ans LCM (4,6)
- Two traffic lights blink at an interval of 40 and 60 seconds respectively. After how many minutes will they link together? Ans LCM (40,60).
- HCF is also important for remainder related questions. but I’ll cover that in a separate article.
- How to apply LCM in time-speed-distance/work, pipes-cistern etc questions, is already covered in old articles. (Mrunal.org/aptitude)
How to find LCM using Prime-Factorization?
Suppose in the exam, we need to find LCM of 4 and 6.
Make a table like this
| Number | Factors |
| 4 | |
| 6 |
Now you need to find the prime factors of 4 and 6.
| Number | Factors |
| 4 | 2 x 2 |
| 6 | 2 x 3 |
Express it in terms of “powers”. For example 2 x 2 =22
| Number | factors |
| 4 | 22 |
| 6 | 2 x 3 |
Now make the third row called “LCM”.
| Number | factors |
| 4 | 22 |
| 6 | 2 x 3 |
| LCM |
Now write all prime numbers in this “LCM row”
| Number | factors |
| 4 | 22 |
| 6 | 2 x 3 |
| LCM | 2, 3 |
Write maximum power of each prime number
| Number | factors |
| 4 | 22 |
| 6 | 2 x 3 |
| LCM | 22, 3 |
As you can see, maximum power of 2 was 22 (in 4’s row).
Now multiple the numbers given in LCM row
| Number | factors |
| 4 | 22 |
| 6 | 2 x 3 |
| LCM | 22 x 3 =12 |
That’s our answer. LCM (4,6)=12.
If I plot this LCM situation on a Venn Diagram, it’ll look like this:

Anyways, Let’s try a difficult one: 56 and 96.
LCM of two numbers (56, 96)
| Numbers | Factors |
| 56 | |
| 96 |
First recall, in which tables do they come? Well 56 comes in 8’s table and 96 comes in 12’s table.
| Number | Factors |
| 56 | 8 x 7 |
| 96 | 12 x 8 |
- but we need factors in “prime number” format. 12 and 8 are not prime numbers. So let’s Simplify further.
- 56 = 8 x 7 = 23 x 7 (; because 8 = 4 x 2 = 2 x 2 x 2)
- 96 = 12 x 8 = (4×3)x(4×2)=( 22x3) (23)=25x3 (please note you have to do this things in your head, if you start making every calculation on a piece of paper, you’ll run out of time in the exam).
| Number | Factors |
| 56 | 23 x 7 |
| 96 | 25x3 |
Now let’s make the LCM row. Write all prime numbers (2,3 and7) in ascending order.
| Number | Factors |
| 56 | 23 x 7 |
| 96 | 25x3 |
| LCM | 2 3 7 |
Now write maximum powers of each prime number.
| Number | Factors |
| 56 | 23 x 7 |
| 96 | 25x3 |
| LCM | 25 3 7 |
Multiply these numbers
| Number | Factors |
| 56 | 23 x 7 |
| 96 | 25x3 |
| LCM | 25 x3x7=32×21=672 |
So LCM (56,96)=672
let’s try finding LCM of three numbers.
LCM of three numbers: (12,15,20)
Approach is same. Make prime factors
| Number | Prime factors |
| 12 | 22 x 3 |
| 15 | 3 x 5 |
| 20 | 22 x 5 |
Make a new row, write all prime factors in ascending order.
| Number | Prime factors |
| 12 | 22 x 3 |
| 15 | 3 x 5 |
| 20 | 22 x 5 |
| LCM | 2,3,5 |
In the last row, Write the maximum power of those prime numbers.
| Number | Prime factors |
| 12 | 22 x 3 |
| 15 | 3 x 5 |
| 20 | 22 x 5 |
| LCM | 22, 3, 5 |
Now multiple the numbers in last row
| Number | Prime factors |
| 12 | 22 x 3 |
| 15 | 3 x 5 |
| 20 | 22 x 5 |
| LCM | 22x3x5=60 |
Therefore LCM (12,15,20)=60.
You can also look at it in following way:
- 12 x 5 = 60
- 15 x 4 = 60
- 20 x 3 = 60.
So 60 is the least common multiple.
LCM of prime numbers
Find LCM of 7,11,13
We already know these are prime numbers. So they’ll not have any common factors. We just have to multiply them together and we’ll get LCM. But for the sake of conceptual clarity
| Numbers | Factors |
| 7 | 7 x 1 |
| 11 | 11 x 1 |
| 13 | 13 x 1 |
| LCM | 1x 7 x 11 x 13 =1001 |
So 1001 is the answer.
LCM of co-prime numbers
- Co prime numbers are those numbers that donot have any common factors. For example, 14 and 15.
- Individually none of them is prime number because 14=2 x 7 and 15 = 3 x 5.
- But they (14 and 15) donot have any common factors. So they’re called co-prime numbers (when they’re given together).
- Any two consecutive numbers are co-prime numbers. (e.g. 11,12 or 1548,1549).
- In case of co-prime numbers, just multiply them and you will get LCM. There is no need to find factors. example
| 6 | 2 x 3 |
| 7 | 7 |
| LCM | 2 x 3 x 7 = (6)x7 =42 |
Advantages of this method?
- Extremely fast when you’ve to find LCMs of two digit numbers for example 12,15,96.
- And usually in time speed work, pipe-cistern type questions have number in two digits (e.g. 12, 15, 96)…so it is very easy to recall in which multiplication tables do they come.
Disadvantages?
- Becomes tedious, as the number grows bigger, for example LCM (235, 512). There are other methods to solve those LCMs, but let’s not complicate this article any further. Let’s stick to this Prime-Factorization method for a while.
Ok so far we know what is LCM and how to find HCF/GCD?
What is HCF or GCD?
- HCF= Highest common factors.
- GCD= Greatest common divisor. Names are different otherwise they’re one and same.
- Suppose you’ve to find the HCF of (4 and 6).
- I’ll write the tables of numbers that come before 4 and 6 (i.e. 1, 2 and 3.)
| 1 x 1 = | 1 | 2 x 1 = | 2 | 3 x 1 = | 3 |
| 1 x 2 = | 2 | 2 x 2 = | 4 | 3 x 2 = | 6 |
| 1 x 3 = | 3 | 2 x 3 = | 6 | 3 x 3 = | 9 |
| 1 x 4 = | 4 | 2 x 4 = | 8 | 3 x 4 = | 12 |
| 1 x 5 = | 5 | 2 x 5 = | 10 | 3 x 5 = | 15 |
| 1 x 6 = | 6 | 2 x 6 = | 12 | 3 x 6 = | 18 |
| 1 x 7 = | 7 | 2 x 7 = | 14 | 3 x 7 = | 21 |
| 1 x 8 = | 8 | 2 x 8 = | 16 | 3 x 8 = | 24 |
| 1 x 9 = | 9 | 2 x 9 = | 18 | 3 x 9 = | 27 |
Ok, in which number’s table (1, 2 or 3) do you see both 4 and 6 reappearing?
There are two such tables 1’s table and 2’s table.
| 4 and 6 are common in 1’s table. | 4 and 6 are common in 2’s table. |
| 1 x 4=4 | 2 x 2=4 |
| 1 x 6=6 | 2 x 3=6. |
What does ^this mean?
- If I divide 4 by 1, I get zero remainder. Similarly if I divide 6 by 1, I get zero remainder. In other words, 1 is the factor of both 4 and 6. In other words, 4 and 6 come in the table of 1.
- Similarly, If I divide 4 by 2, I get zero remainder. Similarly if I divide 6 by 2, I get zero remainder. In other words, 2 is the factor of both 4 and 6. In other words, 4 and 6 come in the table of 2.
- Thus, 4 and 6 have two common factors (1 and 2) but highest of these common factors is 2. Therefore HCF of (4,6)=2.
HCF 4 EXAM?
- What is the highest number that’ll divide 4 and 6 evenly. Ans HCF (4,6)
- There is a 4 x 6m rectangular farm. Find the length of longest tape that can measure this field. Ans HCF (4,6)
- There is a 4x 6cm floor. Find the length of largest square tile that can be evenly laid on it. Ans HCF (4,6)
- Two drums contain 400 and 600 liters of desi and foreign liquor respectively. What is the biggest measure (cup) that can measure both of them exactly? Ans. HCF (400, 600).
- A teacher has 40 pens and 60 pencils. Find maximum number of students among whom she can distribute these items evenly.
- HCF is also important for remainder related questions. but I’ll cover that in a separate article.
HCF finding: Prime Factorization
In the exam, we can’t make multiplication tables of every number preceding the given numbers! So here is the shortcut technique. We’ll use the same approach we’ve used in LCM method: prime factorization.
HCF of two numbers (4, 6)
First make prime factors of given numbers.
| 4 | 22 |
| 6 | 2 x 3 |
Now, make third row: HCF and write the prime numbers that are common in both numbers.
| 4 | 22 |
| 6 | 2 x 3 |
| HCF | 21 |
Therefore, HCF (4,6)=2
If I’ve to plot the HCF of 4 and 6 on a Venn diagram, it’ll look like this:
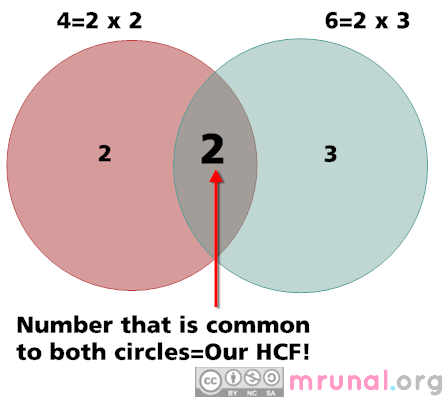
HCF of three numbers (12,24,36)
| 12 | 2 x 6 |
| 24 | 3 x 8 |
| 36 | 6 x 6 |
But I want them in prime format. So I’ll further simplify.
| 12 | 2 x 2 x 3=22 x 3 |
| 24 | 3 x 2 x 2 x 2=23 x 3 |
| 36 | 3 x 2 x 3 x 2=22 x 32 |
In the exam you’ve to do this in your ^head.
| 12 | 22 x 3 |
| 24 | 23 x 3 |
| 36 | 22 x 32 |
Now make a new row, write the prime numbers that are common in all of above.
| 12 | 22 x 3 |
| 24 | 23 x 3 |
| 36 | 22 x 32 |
| HCF | 22x3 |
^in case you’re confused, let me rewrite and do it again
| 12 | 22 x 3 |
| 24 | 22 x 2 x 3 |
| 36 | 22 x 3 x 3 |
| HCF | 22x3 |
The numbers highlighted in bold are common. Therefore HCF = 22 x 3=12.
HCF of prime numbers (13,29)
Prime numbers donot have any common factors. So HCF of such numbers is always 1. But for the clarity let’s do it
| 13 | 13 x 1 |
| 29 | 29 x 1 |
| HCF | 1 (because 1 is common in both) |
HCF of co-prime numbers (12,25)
Again same: 1, because co prime numbers donot have common factors.
Similarly consecutive numbers (like 456,457) donot have common factors either.
Therefore, in all such cases, HCF =1.
HCF vs LCM: #1 multiplication
If we’ve two numbers a and b. and their HCF and LCM are given then
HCF x LCM = a x b.
But this relation only work for TWO numbers and not for more than two numbers.
Let’s understand this with an example.
You know that LCM (4,6)=12 and HCF (4,6)=2.
| Left hand side (LCM x HCF) | Right hand side (multiplication of given numbers) |
| 12 x 2 | 4 x 6 |
| =24 | =24 |
So both sides match. Therefore, in case of two numbers (a and b)
LCM X HCF = a x b.
But this is not always true for three numbers. For example, Find LCM and HCF of 12,15,20. You’ll get HCF=1 and LCM=60.
| Left hand side (LCM x HCF) | Right hand side (multiplication of given numbers) |
| 60 x 1 | 12 x 15 x 20 |
| =60 | =3600 |
In this case, both sides donot match.
HCF vs LCM: #2 Magnitude
For any given numbers, their LCM is always greater than or equal to the biggest number. For example
| Numbers | LCM |
| 12,15,20 | 60 so greater than biggest number (20) |
| 15,30 | 30. which is equal to the biggest number (30). |
Similarly, for HCF, the HCF of given numbers is always less than or equal to the smallest number. For example
| Numbers | HCF |
| 12,15,20 | 1 so it is smaller than smallest number 12 |
| 15,30 | 15. so it is equal to the smallest number 15. |
Ok this is just the basic overview. In the next article, we’ll see the application of these concepts. In the mean time, try finding LCM and HCFs of following numbers
| Question | Answer (LCM, HCF) |
| 91, 12 | 1092, 1 |
| 46, 69 | 138, 23 |
| 69, 97 | 6693, 1 |
| 63, 33 | 693, 3 |
| 72, 58 | 2088, 2 |
| 5, 84 | 420, 1 |
| 91, 41 | 3731, 1 |
| 65, 57 | 3705, 1 |
| 74, 12 | 444, 2 |
| 44, 55 | 220, 11 |
| 8, 28, 175 | 1400, 1 |
LCM, HCF of fractions
Just observe the color pattern in following image:

for more practice on LCM, HCF
| Book | Chapter no. |
| Quantitative Aptitude, R.S.Agarwal | 2 |
| Fast track Arithmetic, Rajesh Verma | 2 |
| Quantam CAT, Sarvesh Kumar | Ex.1.3, 1.4 |
| Arun Sharma (CAT) | 1 |
In all such books, the authors first give 5-6 illustration examples and then exercises. I suggest you solve the the illustration examples as well. After all aptitude is all about practice.

![[Reasoning] Calendar Questions: Finding day or date, concepts, shortcuts explained](https://mrunal.org/wp-content/uploads/2013/01/i-lr-500x383.png)
Very nicely written!! Thank you for the knowledge shared.
Hcf and lcm gives us alot of concepts to find hcf and lcm quickly
It is very helpful to clear the concept of LCM and HCF. Thank you!!!!
Hcf and LCM shortcut method …..please sir…
If the sum of two number is 55 and the hcf and LCM of there number are 5and120 respectively then the sum of reciprocals of the number is equal of.. A)55/120 b)60/55 c)11/120,d)120/11 please sir explain answer sir……
c) 11/120
Let the numbers be a and b.
Then, a + b = 55 and ab = 5 x 120 = 600.
The required sum = 1/a+1/b=a+b/ab=55/600=11/120
LCM &HCF are those factor which are easily to understand the mathematics concept
how to calculate hcf and lcm by simple calculation
The sum of two no is 100 theirs LCM IS 120 HCF?
use difference method for hcf and lowest factor method for lcm contact me 8770870682 for tricks of number system ,prime number
Your concept is very good.
very good concept
what is the lcm of 60,75
Really it helps me a lot thanks you