1. Prologue
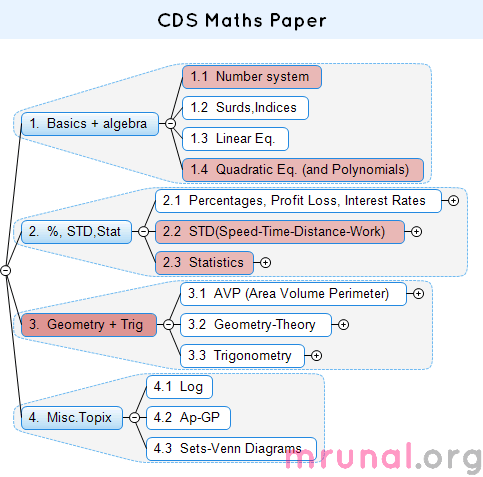
  2. Topic wise breakup CDS Maths Papers
  3. Gather the weapons
  4. Warm up the brain
  5. [Block#1]: Basics + Algebra
  6. Number System
  7. Surds, Indices, Powers, Exponents
  8. Linear Equations
  9. Quadratic equations
  10. Appendix Download link: Topic wise Sorted NCERTs

Prologue

Studyplan for CDS GK paper already given click me. In this three part article series, we’ll how to prepare for the maths papers. This is different from CSAT and CAPF in following ways:

  1. No questions on reasoning.
  2. Plenty of questions Trigonometry, quadratic equations asked.
  3. They ask theory based geometry i.e. beyond the routine area-volume-perimeter type questions that you see in bank, LIC and state service exams.
  4. Even Statistics based theory questions are asked.

In recent years, SSC CGL has been moving towards Trigonometry, Geometry and Quadratic equations. CDS runs on parallel tract, but with higher difficulty level.

Topic wise breakup CDS Maths Papers

Duration: 2 hours; 100 MCQs; 100 Marks; Negative-Marking for wrong answers: yes.

Block CDS Exam 2012(I) 2012(II) 2013(I) 2013(II)
BASICS: need to be prepared for any aptitude exam. BoDMAS/Simplification 2 1 1 0
surds indices 2 3 2 5
number system 12 11 7 11
linear equation 3 3 3 2
BANK: these topics are important for Bank, IBPS, LIC, PSU type exam. % (profit loss, Interest rate) 5 7 2 2
Ratio-Proportion 1 1 1 0
Mixture-Alligiation 0 0 2 1
statistics, Data Interpretation 6 7 7 5
Time-Speed-Distance-Work 3 5 9 10
SSC|CDS block: more than 50% of the Questions come from this block. quadratic equations 11 9 13 13
Trigonometry 10 14 18 14
Geometry 39 34 33 36
Misc: asked in SSS/CDS/CAT. This should be prepared at last, once you’re done with priority topics viz. trig, QE and geometry. functions, Coordinate Geometry 2 1 0 0
logarithms 3 2 0 0
Venn Diagrams 1 2 2 1
total MCQs in CDS 100 100 100 100

Let’s plot this data on a graph.
CDS Maths Papers (Topicwise Breakup)

From the above graph you can see in last two papers 2013(I) and 2013(II) nearly 80% of the questions came from only five topics viz.

  1. Number System
  2. Quadratic Equations (And Polynomials)
  3. Time-Speed-Distance-Work
  4. Geometry
  5. Trigonometry

so the only question remains is: how to prepare?  I’m dividing it into four blocks, as show in the following chart. Topics highlighted in red, are high priority.

CDS-Maths-topics

in this article, we’ll see how to handle block#1.

  • Now in the second article, we’ll see how to approach block#2: percentage, profit-loss, simple-compound interest rate, time-speed-distance-work and statistics-Data interpretation related problems. click me
  • in this third and last article, we’ll see block#3: how to approach geometry, trigonometry and remaining misc. Topics(block#4) .click me

But first….

Gather the weapons

ESSENTIAL
  1. NCERT Maths (required for definition-theory based MCQs). Topicwise zip file given at bottom
  2. One book on quantitative aptitude*
  3. one separate notebook to maintain “diary of mistakes”
OPTIONAL
  1. Topicwise solved paperset of previous CDS exams (Arihant Publication)
  2. A folder and loose A4 sized papers. (To maintain a diary of mistakes and shortcuts. This is better than a notebook because you can add new pages anywhere as per your requirement.)
  3. A slate, like those poor kids use in government primary schools. (It saves lot of paper wasted in practicing math sums.)

*Which book to use for CDS Maths?

Book-Cover-Quantam CAT Sarvesh

NCERTs only clear the basics but for competitive exam level maths, you need a book on quantitative aptitude to learn and practice advanced concepts.  In the market there are plenty of names. My recommendation is as usual Quantam CAT by Sarvesh Kumar Verma.Reasons:

  1. RS Aggarwal, M.Tyra, Guha etc. don’t cover geometry theory (cords, bisectors, orthocenter etc.);  trigonometry, quadratic equations, logarithms, etc. in detail.  While they help for bank, LIC level exams but hardly useful for CDS.
  2. Sarvesh Kumar’s geometry chapter is thorough, particularly the summary tables of triangles, quadrilaterals and circles. Those of you already know the basics of geometry, can directly use without having to go through NCERTs.
  3. For the given price range this book helps in all competitive exams: starting from SSC CGL, PSU, IBPS, UPSC to all the way upto CAT.  Each chapter contains introductory exercises, level 1, level2 and final round exercises. For CDS do upto level 1. Thus saves your time and money in not having to buy new book for every exam.

Warm up the brain

In CDS, there is minimum physical requirements for height, chest, eyesight. Similarly to glide through Maths paper, you need to meet following requirements:

Minimum:

  1. Memorize the multiplication tables of 2 to 9; 12, 15, 16 and 25.
  2. Memorize squares upto 19 and cubes upto 9. (necessary for number system, HCF-LCM and divisibility related MCQs )

Preferred:

  1. Memorize the multiplication tables of 2 to 9; 12 to 25; finally 29
  2. Memorize squares upto 29 and cubes upto 15.
  3. Memorize all prime numbers between 1 to 100
  4. Trachtenberg’s speed multiplication rules for 5, 9 and 11. (http://en.wikipedia.org/wiki/Trachtenberg_system)
  5. two digit long division click me

Note: An excel file containing multiplication tables and prime numbers in given the NCERT zip file itself.

[Block#1]: Basics + Algebra

Under this block: total four areas

topic priority avg.MCQs in each of the last four CDS exams
  1. Number system
 high 10
  1. surds indices
 medium* 3
  1. linear equations
 medium* 3
  1. quadratic equations (and polynomials)
 high 11

*although barely 3 MCQs are asked, still you need good grip over them, because indirectly these concepts are essential for solving other MCQs in compound interest rate, profit loss, quadratic eq. etc.

Number System

In CDS paper, a good number of questions directly come from theory/definitions. Hence NCERTs important. Example:

Q. The set of integers is closed with respect to which one of the following?

  1. Addition only
  2. Multiplication only
  3. Both A and B
  4. Division

You’ll find the answer in Class 7 NCERT. I’ve arranged the NCERT maths chapters from class7 to 10 (+a few from 11) topic wise according to their utility in the aptitude exams. Zip file is at bottom. Even in worst case scenario, at least go through the Summary at the end of each chapter. And don’t just ‘read’ the NCERT- solve all the sums given in it, including the illustrations and examples.

Secondly, I’m providing reference tables about the NCERT chapters for each topic. Abbreviations:

  • “7_1 integers”= class 7 maths textbook, chapter 1
  • DQ=direct questions asked in CDS from the theory/definition/examples given in this chapter. Hence even if you “know” the topic, DO go through those chapters.
  • IAK=”I already know”. Meaning you can ignore this chapter, if you’re basics are already good. (i.e. you’ve already cleared written stage of bank, SSC or LIC.)
  • ICD=”I can’t do”. Meaning you the theory/ concept is just not going inside your head. versus barely 1-2 MCQs are asked from that particular in CDS exam. Then you take ‘risk’ to ignore/skip. As such I don’t recommend you skip anything but at the same time, there is no point in being stuck at just one topic when exam is just ~eight weeks away from now. (9 Feb.2014)
  • “Bold”: topics highlighted in bold are MUST DO, Most important because MCQs routinely appearing from there.

Here starts the first table.

7_1 Integers number line and properties of integers (associative, distributive etc) DQ
7_2 Fractions and Decimals proper and improper fractions, comparing fractions IAK
7_9 Rational Numbers comparing rational numbers IAK
8_1 Rational number table 1.2 (properties of rational numbers) very important for MCQs. DQ
8_16 Playing with Numbers Reversing digits. DQ
Divisibility rules for 2,3,5,9 IAK
9_1 Number systems recurring decimals DQ|IAK
real numbers- geometry connection DQ
10_1 Real Numbers Euclid’s division algorithm ICD*
Irrational numbers, prime numbers DQ

*Euclid’s division algorithm helps finding HCF-LCM of big numbers quickly but if it’s not going in your head (=”I can’t do”), then you can just use desi-method to find HCF-LCM (i.e. via factorization).

After this is done,

  1. https://mrunal.org/2013/03/aptitude-lcm-hcf-gcd-basic-concept-calculation-applications-explained.html
  2. https://mrunal.org/2013/01/aptitude-remainder-one-number-and-two-divisors-number-theory.html

Lastly Sarvesh Kumar’s chapter on fundamentals.  focus especially on the following topics

  1. Divisibility rules- with special focus on (7,11,13,17,19,23) Because for prime number related MCQs you’ll need it. then solve all the MCQs in his first introductory exercise
  2. properties of squares
  3. table of prime numbers from 1-100
  4. How to test whether a number is prime or not? what is co-prime, what is composite number?
  5. rules of simplification or calculation (BODMAS)
  6. Remainders
    1. HCF with remainders
    2. LCM with remainders
  7. HCM and LCM of fractions and decimals
  8. square roots and cube roots of fractions
  9. recurring decimals
  10. conjugate surds and the sums related to them
  11. concept of unit digit (e.g. what is the unit digit of 235)

You may ignore following topics from his chapter on fundamentals

  1. Concept of remainder in huge numbers (e.g find remainder when 5123 divided by 7)
  2. imaginary numbers, complex numbers (i=root minus1)
  3. mth root of unity
  4. digital number systems (converting decimal into binary etc)
  5. coding decoding

now let’s check the…

Demo MCQs from previous CDS exams

NUMBERS CLASSIFICATION PRIME NUMBER
  1. If n is a natural number then root “n” is
    1. always natural
    2. always rational
    3. always irrational
    4. either a natural or an irrational number
  2. ABC is a triangle, AD perpendicular to BC. If AB, BC and CA lengths are rational numbers then
    1. AD and BD must be rational
    2. AD must be rational but BD need not be rational
    3. BD must be rational but AD need not be rational
    4. neither AD nor BD need be rational
  3. If x is positive even integer and y is negative odd integer, then xy is (odd, even, rational, none of above)
  1. Every prime number of the form 3k +1 can be represented in the form 6m + 1(k, m are integers) when
    1. k is odd
    2. k is even
    3. k can be both odd and even
    4. No such form is possible
  2. Find correct statement
    1. To obtain prime numbers less than 121, we are to reject all the multiples of 2, 3, 5 and 7.
    2. Every composite number less than 121 is divisible by a prime number less than 11.
    3. both A and B
    4. None
  3. Which of the following is composite number? (589, 569, 571,563)
  4. Which of the following is a prime? (161, 171, 173, 221)
DIVISIBILITY RELATED REMAINDER THEOREM RELATED
  1. The number 22222 is divisible by
    1. 3 but not by 7
    2. 3 and 7 but not 11
    3. by 2, 7 but not 11
    4. by 3,7 and 11
  2. among the following, which is the largest four digit number divisible by 88 (options: 9988, 9966, 9944, 8888)
  3. 195 +215 is divisible by    (10, 20, both, none)
  1. Number divided by 2,3 or 5 gives remainder 1. the number is : (31, 47, 49,53)
  2. What is the sum of positive integers less than 100, which leaves a remainder 1 when divided by 3 and leaves a remainder 2 when divided by 4? (416, 620, 1250, 1314)
LAST DIGIT RECURRING DECIMALS
  1. what is the last digit in the expansion of 2457754
  2. what is the last digit in the expansion of 7402+3402
 (Note in following number, assume underline is “bar” above the number.)

  1. what is the value of 3.76-1.4576
  2. If 2.5252525….. =(p/q) then what is the value of q/p

HCF-LCM variety of questions

GENERIC REAL LIFE SITUATIONS
  1. If HCF of two positive integers is 24, then LCM cannot which of the given values?
  2. for two numbers, if LCM=14 x HCF and LCM+HCF=600 and if one number is 80 what is the other number?
  3. For any integer n, what is the HCF of integer m=2n+1 and k=9n+4?
  1. 21 mange trees, 42 apple trees and 56 orange trees are to be planted in rows such that each row contains same number of trees of one variety only. what is the minimum number of rows in which the above trees may be planted?
  2. 5 bells start tolling together, and toll at intervals of 2,4,68 and 10 respectively. how many times do the five bells toll together in 20 minutes?
FRACTIONS AND DECIMALS POLYNOMIALS**
  1. what is the LCM of (2/3),(7/9),(14/15)
  2. what is the HCF of 3.0, 1.2, 0.06
  1. what is the HCF of polynomials x4-3x+2, x3-3×2+3x-1  and x4-1
  2. what is the LCM of a3b-ab3, a3b2+a2b3 and ab(a+b)

**for this type of MCQs, first go through quadratic equations related block.

Surds, Indices, Powers, Exponents

7_13 Exponents and Powers comparing numbers with powers, how even-odd powers change the sign of negative numbers, expressing large numbers in std.form IAK
8_06 Squares and Square Roots finding square root through repeated subtraction, square roots of decimals, estimating square root DQ
8_07 Cube and Cube Roots finding cube roots ICD
8_12 Powers laws of exponents, expressing numbers in standard form. DQ

Demo MCQs from previous CDS exams

comparing quantities solving unknown powers
Which is the smallest number of the following?

  1. [(5-2)-2]-2
  2. [(5-2)2]-2
  3. [(2-5)-2]-2
  4. [(2-5)2]-2

Which of the following is largest?

  1. root2
  2. cube root of 3
  3. 61/6
  4. 121/12
  1. If 16 x 8(n+2)=2m, then what is the value of m?
  2. if 27 x 81(2n+3)-3m=0 then what is the value of m?
  3. if ax=by=cz and abc=1 then what is the value of xy+xz+yz?
finding roots**
  1. what is the square root of 9+2root14
  2. what is the square of (2+root2)

for these type of MCQs, first go through quadratic equation block.

Linear Equations

@Those from Science/engineering background: directly goto Sarvesh Kumar=>chapter on “Elements of Algebra” =>Linear Equation. Mugup the theory bullets, do all the examples, introductory exercises and level1.

@Those from non-science  stream and/or very weak in Maths:

Linear equation means unknown variable (x or y) doesn’t have anything above their ‘head’.  e.g.

x2+2x+1 This is not linear equation because x has “2” above its head.
2x+1 This is linear equation because x doesn’t have anything above its head. (Actually its x1 but for our understanding purpose, take it as just “x”)

Linear equations are very important for aptitude exams. Both as ‘direct MCQs’ (for age, salary, spending related problems) as well as indirect applications in Geometry; time-speed-distance-work; profit-loss-SI-CI problems etc. first go through following NCERT chapters:

7_4 Simple Equations how to convert statements into simple equation. IAK
7_12 Algebraic Expressions MONOMIALS, BINOMIALS, TRINOMIALS AND POLYNOMIALS DQ
7_12 Algebraic Expressions adding-subtracting simple equations IAK
8_2 Linear Equation Age based questions DQ|IAK
8_2 Linear Equation Notes and coins denominations DQ|IAK
10_3 Pair of Linear Equations in Two Variables
  1. In what situation, infinite solution / no solutions?  Table 3.4 most important for MCQs.
DQ
  1. algebraic method to solve equations
 DQ
  1. cross multiplication method to solve equations
 ICD

Then goto Sarvesh Kumar=>chapter on “Elements of Algebra” =>Linear Equation. Mugup the theory bullets, do all the examples, introductory exercises and level1

Two things to be kept in mind, while solving questions on linear equation:

#1: keep minimum variables

Suppose the question runs like this “The sum of present ages of father and son is 56, and 5 years ago Son’s age was……….blah blah blah….find the present age of Father. ”

avoid this do this
  • assume father’s present age “f”
  • son’s present age “s”
  • assume father’s present age “f”
  • assume Son’s present Age=(56-f)
  • here you assumed two variables “f” and “s”= lengthier calculations and chances of mistakes.
  • here you’ve to worry about only one variable “f”

#2: Cannot be determined

Suppose you end up with two equations like this:

  1. x+y=5
  2. y+z=6

Here you’ve two equations but three variables (x, y and z). You can never find out the unique value of  x, y, z in such situation. Hence answer = “Cannot be determined”.

But sometimes, even two variable-two equation set can be impossible to solve. For example

No solution infinite solution
  1. x+ 2y=4
  2. 2x+ 4y= 12
 2x+ 3y=94x+ 6y=18

To learn more about ^this, refer to NCERT Maths Class 10, Chapter3, table given on the page #9. CDS directly asks MCQs from this.

Linear equations: Variety of MCQs

From previous CDS exam

Age digit reversal / unknown numbers
  1. 10 years back, Ram was five times as old as Shyam but 20 years later from now, he will be only twice as old as shyam. find the present age of shyam.
  2. Two years back, mom was 8 times old as her daughter. After one year mom ‘s age will be five times of daughter’s. After how many years from now, mom’s age will be 3 times the daughter’s age?
  1. A number consists of two digits, whose sum is 10.If 18 is subtracted from the number, and digits of the number are reversed. What is the product?
  2. The sum of two numbers is 80. If the larger number exceeds four times the smaller by 5, what is the smaller number?
Nature of solutions nature of solutions
The system of equations x+2y=3 and 3x+6y=9 has?

  1. unique solutions
  2. no solution
  3. infinite number of solutions
  4. finite number of solution
 Under what condition do the equation kx-y=2 and 6x-2y=3 have a unique solution?

  1. k=3
  2. k not equal ot 3
  3. k=0
  4. k equal to 0

Quadratic equations

High priority topic, ~11 MCQs each year in last four exams.

8_9 Algebraic Expressions Polynomials: additions, subtraction, multiplication. IAK
8_14 Factorization making Factors of the form (x + a) (x+ b); division of polynomials IAK
9_2_Polynomials
  • remainders,
  • finding value of “k” in the polynomial equation
 DQ
10_2 Polynomials sum of roots, product of zeros (given on pg.30) DQ
10_4 Quadratic Equations
  • factors of quadratic equations (QE)
  • nature of roots of QE
 DQ

Then Sarvesh Kumar’s chapter on

  1. Elements of algebra. And memorize all the formulas given in this chapter e.g. a3+b3=(a+b)(a2+b2-ab)
  2. Theory of equations. (You may ignore the graphs, maximum minimum values.). Sometimes CDS even asks Quadratic inequalities- it is explained in this chapter, but if that theory is not going in your head then ignore- because at most only one MCQ comes- that too not on regular basis.

For additional practice on polynomials and quadratic equations, you can solve the last three years’ SSC-CGL papers (tier 1 Maths section and Tier II maths paper).

Demo MCQs from previous CDS exams

FACTORS REMAINDERS
  1. If (x4+x-4)=322,what is one of the value of (x-x-1)?
  2. If x2-11x+ a and x2-14x+2a have a common factor, then what are the values of a?
  3. If (a+b=3), then what is the value of (a3 +b3 +9ab)?
  1. If x5 -9x2+12x-14 is divisible by (x-3),what is the remainder?
  2. if px3+3x2-3 and 2x3-5x+p both have same remainders when divided by (x-4) then what is the value of p?
ROOTS HCF, LCM
  1. If one root of the equation 2x2+3x+c=0 is 0.5, then what is the value of c?
  2. If one root of the equation ax2+x-3=0 is -1,then what is the other root?
  3. What is the least integral value of k for which the equation x2-2(k-1)x + (2k+1)=0 has both the roots positive?
  4. For what of k,will the roots of the equation kx2-5x+6=0 be in the ratio of 2:3?
  1. If HCF of x3+mx2-x+2m and x2+mx-2 is a linear polynomial then what is the value of m?
  2. what is the LCM of 6x3+60x2+150x and 3x4+12x3-15x2

This concludes the block#1. In the next article, we’ll see how to approach block#2 (%, profit loss, SI-CI, time-speed-work).

Appendix Download link: Topic wise Sorted NCERTs

You’ve two choices

Choice #1: good internet connection: And you want to download entire zip file at once (size 35MB) then use following link: https://files.secureserver.net/0sYHJ029rgUbrg

Choice #2: not so good internet connection: and / or You want to download small zip files or selective topics only, then goto following link (e.g. geometry zip file separately, trigonometry zip file separately and so on) then use following link: https://files.secureserver.net/0fmaNqqBDslHlc